Table Of Content

The common use of this design is where you have subjects (human or animal) on which you want to test a set of drugs -- this is a common situation in clinical trials for examining drugs. We want to account for all three of the blocking factor sources of variation, and remove each of these sources of error from the experiment. An assumption that we make when using a Latin square design is that the three factors (treatments, and two nuisance factors) do not interact. If this assumption is violated, the Latin Square design error term will be inflated. The partitioning of the variation of the sum of squares and the corresponding partitioning of the degrees of freedom provides the basis for our orthogonal analysis of variance.
2 Randomized Complete Block Designs
Deciphering the association between sample characteristics, e.g.,tumor types, and the proteome holds the key for improved diagnosticand treatment of diseases. The explanatory variables of interest are alsoreferred to as treatment variables, e.g., treatment, disease status,or tumor type. With a randomized block experiment, the main hypothesis test of interest is the test of the treatment effect(s). Every binary matrix with constant row and column sums is the incidence matrix of a regular uniform block design.
Lesson 4: Blocking
But if some of the cows are done in the spring and others are done in the fall or summer, then the period effect has more meaning than simply the order. Although this represents order it may also involve other effects you need to be aware of this. A Case 3 approach involves estimating separate period effects within each square.
Design of complex neuroscience experiments using mixed-integer linear programming - ScienceDirect.com
Design of complex neuroscience experiments using mixed-integer linear programming.
Posted: Wed, 05 May 2021 07:00:00 GMT [source]
ANOVA: Yield versus Batch, Pressure
The sequential sums of squares (Seq SS) for block is not the same as the Adj SS. We could select the first three columns - let's see if this will work. Click the animation below to see whether using the first three columns would give us combinations of treatments where treatment pairs are not repeated. Is the period effect in the first square the same as the period effect in the second square? If it only means order and all the cows start lactating at the same time it might mean the same.
Book traversal links for 8.9 - Randomized Block Design: Two-way MANOVA
As an example, let's take any 3 columns from a 4 × 4 Latin Square design. This subset of columns from the whole Latin Square creates a BIBD. This is a Case 2 where the column factor, the cows are nested within the square, but the row factor, period, is the same across squares. Together, you can see that going down the columns every pairwise sequence occurs twice, AB, BC, CA, AC, BA, CB going down the columns. The combination of these two Latin squares gives us this additional level of balance in the design, than if we had simply taken the standard Latin square and duplicated it.
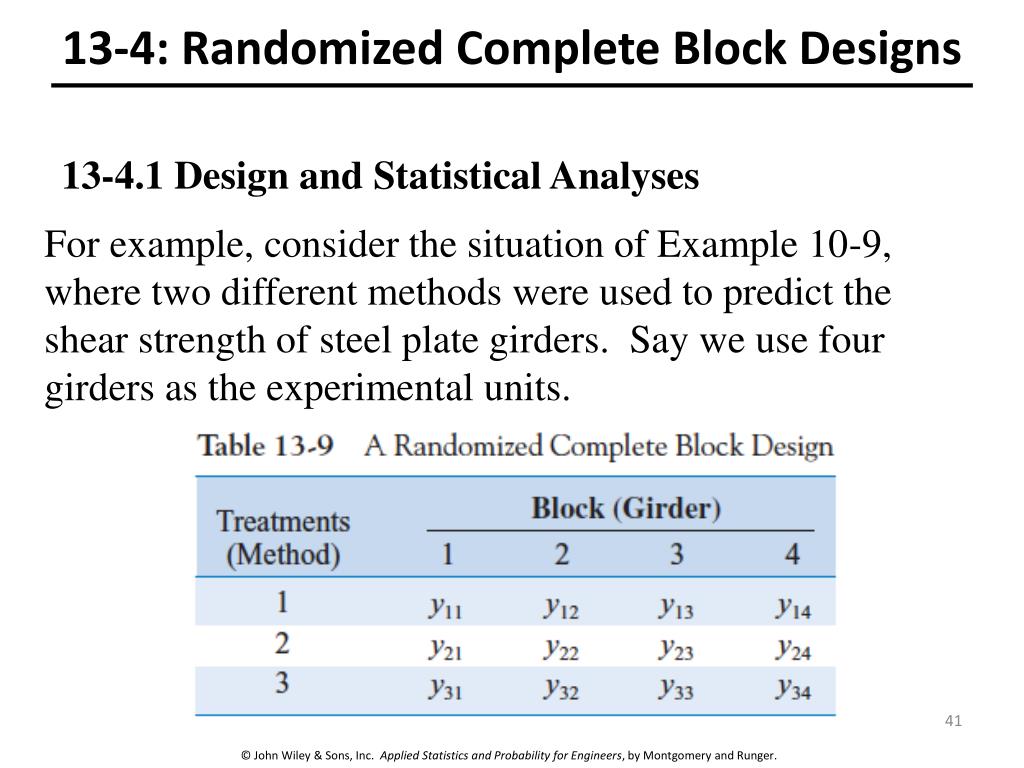
This design allows us to fully remove thebetween-block variability, e.g., variability between different locations, fromthe response because it can be explained by the block factor. In that sense, blocking is a so-calledvariance reduction technique. A Randomized Complete Block Design (RCBD) is defined by an experiment whose treatment combinations are assigned randomly to the experimental units within a block. Generally, blocks cannot be randomized as the blocks represent factors with restrictions in randomizations such as location, place, time, gender, ethnicity, breeds, etc. It is not simply possible to randomly assign a particular gender to a person.
Partially balanced designs (PBIBDs)
In addition to the experimental error reducing ability, the design widens the generalization of the study findings. For example, if the study contains the place as a blocking factor, the results could be generalized for the places. A fertilizer producer can only claim that it is effective regardless of the climate conditions when it is tested in various climate conditions. Note that the categorized version is solely created forblock allocation, and the final analysis still uses the original variable.
Generally the unexplained error in the model will be larger, and therefore the test of the treatment effect less powerful. A farmer possesses five plots of land where he wishes to cultivate corn. He wants to run an experiment since he has two kinds of corn and two types of fertilizer. Moreover, he knows that his plots are quite heterogeneous regarding sunshine, and therefore a systematic error could arise if sunshine does indeed facilitate corn cultivation.
No Blocking Variable vs. Having a Blocking Variable
The design is balanced having the effect that our usual estimators andsums of squares are “working.” In R, we would use the model formulay ~ Block1 + Block2 + Treat. We cannot fit a more complex model, includinginteraction effects, here because we do not have the corresponding replicates. Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block. We use the usual aov function with a model including the two main effectsblock and variety. It is good practice to write the block factor first; incase of unbalanced data, we would get the effect of variety adjusted for blockin the sequential type I output of summary, see Section 4.2.5and also Chapter 8.
The next thing you need to do after you determine your blocking factors is allocate your observations into blocks. To simplify things, we will assume that you have one main blocking factor that you want to balance over. The objective of the randomized block design is to form groups where participants are similar, and therefore can be compared with each other. The Design Structure has one factor (oven run, Run), and the Treatment Structure two factors (Recipe and Temperature). Because every run has to be a single (nominal) temperature, Temperature and Run must occur at the same level of the experimental design.
Obtained from counting for a fixed x the triples (x, y, B) where x and y are distinct points and B is a block that contains them both. This equation for every x also proves that r is constant (independent of x) even without assuming it explicitly, thus proving that the condition that any x in X is contained in r blocks is redundant and r can be computed from the other parameters. You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. Switch them around...now first fit treatments and then the blocks.
A randomized block design is an experimental design where the experimental units are in groups called blocks. The treatments are randomly allocated to the experimental units inside each block. When all treatments appear at least once in each block, we have a completely randomized block design. It is important to distribute, as best one can,the different levelsof the treatment variables equally over the different levels of thecontrol variables. In case of substantial confounding, as when mostof the subjects receiving Placebo are Female and most of those receiving the Treatment are Male, it can become impossible to estimate the treatmenteffect.
This website is using a security service to protect itself from online attacks. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. In this Latin Square we have each treatment occurring in each period. Even though Latin Square guarantees that treatment A occurs once in the first, second and third period, we don't have all sequences represented.
No comments:
Post a Comment